Questão 159 - ENEM 2010 — Matemática e suas Tecnologias

Professor Janildo Arante

Questão 160 - ENEM 2010 — Matemática e suas Tecnologias *

160

Um balão atmosférico, lançado em Bauru (343 quilômetros a Noroeste de São Paulo), na noite do último domingo, caiu nesta segunda-feira em Cuiabá Paulista,
na região de Presidente Prudente, assustando agricultores da região. O artefato faz parte do programa Projeto Hibiscus, desenvolvido por Brasil, França, Argentina, Inglaterra e Itália, para a medição do comportamento da camada de ozônio, e sua descida se deu após o cumprimento do tempo previsto de medição.

Disponível em: http://www.correiodobrasil.com.br. Acesso em: 02 maio 2010.

Na data do acontecido, duas pessoas avistaram o balão. Uma estava a 1,8 km da posição vertical do balão e o avistou sob um ângulo de 60°; a outra estava a 5,5 km da posição vertical do balão, alinhada com a primeira, e no mesmo sentido, conforme se vê na figura, e o avistou sob um ângulo de 30°.

Qual a altura aproximada em que se encontrava o balão?

a

1,8 km

b

1,9 km

c

3,1 km

d

3,7 km

e

5,5 km

http://hupples.com/#!/grupo/100004/lista/1000025/questao-165

ENEM 2010  QUESTÃO 160

---

Um balão atmosférico, (...).

(Foto: Reprodução/Enem)

Na data do acontecido, (...).

Qual a altura aproximada em que se encontrava o balão?

1. A
     
   1,8km
2. B
     
   1,9km
3. C
     
   3,1km
4. D
     
   3,7km
5. E
     
   5,5km

---

Resolução

Sendo h (em km) a altura aproximada do Balão, tem-se tg30º= logo h=3,11  

RESPOSTA CORRETA:

C

 

3,1km

http://educacao.globo.com/provas/enem-2010/questoes/160.html

D.A. RESOLVE

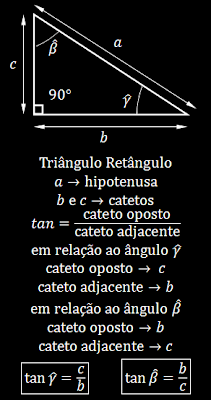
O primeiro passo é relembrar a relação trigonométrica em um triângulo retângulo denominada tangente. O triângulo retângulo possui dois lados que formam o ângulo de 90° chamados de catetos e o maior lado oposto ao ângulo de 90° denominado hipotenusa. Tendo como referência um dos outros ângulos que não o de 90°, a tangente desse ângulo é a razão entre o cateto oposto a esse ângulo e o cateto adjacente ao mesmo, vê-se:

Sabendo o conceito da relação trigonométrica tangente, o segundo passo é aplicá-lo a um dos triângulos retângulos do esquema apresentado. A altura do balão é o cateto oposto aos ângulos de 60° e 30° e as distâncias dos observadores até o pé da altura são os catetos adjacentes, tem-se:

Desta forma, a altura do balão é de, aproximadamente, 3,1 km.

Alternativa C


http://www.da-educa.com/2010/11/plantao-de-duvidas-on-line-orientacoes_30.html