OS BASTIDORES DA HISTÓRIA DA MATEMÁTICA
- BINÔMIO DE NEWTON - INTRODUÇÃO
Para começar a falar sobre binômio de Newton, e posteriormente conhecer e aprender um pouco mais sobre as propriedades que envolvem este conceito, vamos primeiro conhecer um pouco da história de grandes matemáticos, que colaboraram nos estudos da análise combinatória..
Todos sabem que, para ganhar a maioria dos jogos, é necessário sorte, porém podemos, por meio de um cálculo matemático simples usando análise combinatória, calcular as probabilidades de ganharmos fazendo determinadas jogadas, o que de certa forma, pode aumentar consideravelmente as chances de vencer o jogo. Um dos primeiros matemáticos a elaborar estudos sobre o número de combinações possíveis para um determinado fenômeno foi o italiano Niccolo Tartáglia (1500- 1557), que confeccionou uma tabela contendo o número de combinações possíveis no lançamento de dois dados. O desenvolvimento do binômio (1+x)n está entre os primeiros problemas estudados e ligados à Análise Combinatória. O caso n=2 já pode ser encontrado nos “Elementos de Euclides”, em torno de 300 a .C. O “Triângulo de Pascal” era conhecido por “Chu Shih-Chieh ”, na China, (em torno do ano 1300) e antes disso pelos hindus e árabes. O matemático hindu Bháskara (1114-1185?), conhecido geralmente pela "fórmula de Bháskara" para a solução de equações do 2º grau, sabia calcular o número de permutações, de combinações e de arranjos de n objetos. O mesmo aconteceu com o matemático e filósofo religioso francês Levi ben Gerson (1288-1344), que nasceu e trabalhou no sul da França, e que entre outras coisas, tentou demonstrar o5º Postulado de Euclides. O nome coeficiente binomial foi introduzido mais tarde por Michael Stifel-1486?-1567-, que mostrou, em torno de 1550, como calcular (1+x)n a partir do desenvolvimento de (1+x)n-1. Sabemos também que o matemático árabe Al-Karaji - fins do século X - conhecia a lei de formação dos elementos do triângulo de Pascal. Ainda no século XVI, Girolamo Cardano (1501-1576) contribuiu com estudos sobre jogos de azar; além de dar elementos básicos ao cálculo de probabilidades, Cardano desenvolveu mais profundamente as técnicas de contagem de combinações.
Porém, somente no século XVII, foi que Blaise Pascal (1601-1665) e Pierre de Fermat (1601-1665) sistematizaram a análise combinatória.
A FÓRMULA DO BINÔMIO DE NEWTON.
A fórmula do binômio de Newton é a fórmula que dá o desenvolvimento de (x+y)n
Desenvolvendo o binômio (x + y)n, n ∊ ℕ, encontramos:

Toda potência da forma(x+y)n , com x,y ∊ ℜ e n ∊ ℕ, é conhecido como binômio de Newton. O desenvolvimento do binômio de Newton é simples em casos como os seguintes, que você já estudou no ensino fundamental.
Você aprendeu que:
a) (x+y)0 = 1 -1 termo.
b) (x+y)1 = 1x + 1y -2 termos.
c) (x+y)2 = 1x² + 2xy + 1y² -3 termos.
d) (x+y)3 = 1x3 + 3x2y+3xy2 +1y3 -4 termos.
e) (x+y)4 = ?
.
.
.
Um dos processos para determinar (x+y)4 é efetuar o produto (x+y)3 (x+y) que você já conhece e sabe que muita “mão de obra”.
E se continuar aumentando o expoente do binômio. Como fica?
Em casos como (x+y)7 , (2x-y)5 , ( x+2)10 e tantos outros, vamos recorrer à análise combinatória.
Observe os exemplos:

-
O número de termos é dado pelo n+1 termos
O número de termos é dado pelo n+1 termos
- O n é o valor do expoente do binômio
- O expoente de x decresce de n até 0
- O expoente de y cresce de 0 até n.
- O desenvolvimento do binômio (x + y)n é um polinômio.
- O desenvolvimento de (x + y)n possui (n + 1) termos.
- Os coeficientes dos termos eqüidistantes dos extremos, no desenvolvimento de (x + y)n são iguais.
- A soma dos coeficientes de (x + y)n é igual a 2n.
Estas propriedades serão explicadas com mais detalhes nos próximos artigos.
Observação:
Não é necessário memorizar as fórmulas acima, já que elas possuem uma lei de formação bem definida. Vamos ver um exemplo para ficar mais claro:
Vamos tomar como exemplo, o item (d).
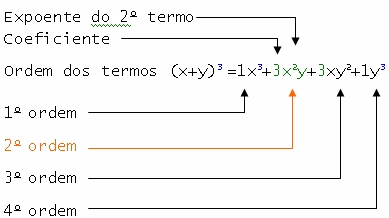
Observe que o expoente do primeiro e últimos termos são iguais aoexpoente do binômio, ou seja, igual a 3.
A partir do segundo termo, os coeficientes podem ser obtidos com a seguinte regra prática de fácil memorização:
Multiplicamos o coeficiente de “x” pelo seu expoente e dividimos o resultado pela ordem do termo. O resultado será o coeficiente do próximo termo. Assim por exemplo,para obter o coeficiente do3⍜ termo do item (d),teríamos:
3.2 = 6; agora dividimos 6 pela ordem do termo anterior 6:2 = 3 que é o coeficiente do 3⍜ termo procurado.
3.2 = 6; agora dividimos 6 pela ordem do termo anterior 6:2 = 3 que é o coeficiente do 3⍜ termo procurado.

Exemplos :
Vamos efetuar o desenvolvimento de :

Em análise combinatória você tem as seguintes conteúdos disponíveis:
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .
Principio aditivo e multiplicativo , fatoriais
Por enquanto ficamos por aqui. Em breve mais atualizações, aguarde!
Se você é aluno, professor, ou simplesmente um apaixonado pela matemática, e quer cooperar com dicas, indicar algum blog legal de matemática, ou que seja relacionado a educação, programas legais que conhece, artigos, trabalhos de escola. Fique a vontade. Mande um e-mail para caco36@ibest.com.br ,ou comente aqui mesmo. Por enquanto ficamos por aqui! Agradeço antecipadamente, comentários, dicas, criticas e sugestões.
Observação:
- Após terminar seus downloads, passe um antivírus antes de abrir seu arquivo.
- Crie um ponto de restauração no Windows, antes de instalar qualquer programa,ou arquivo .
BACHX, A. de; POPPE, L. M. B.; TAVARES; RAYMUNDO N. O. – Prelúdio à Análise Combinatória. Companhia Editora Nacional. 1975
CARVALHO, P. C. P; LIMA, E. L.; MORGADO, A. C; WAGNER, E. – A Matemática do Ensino Médio. Vol. 2. Coleção do Professor de Matemática. Sociedade Brasileira de Matemática. 1998
CARVALHO, J. B. P; CARVALHO, P. C. P; FERNANDEZ, P; MORGADO, A. C de O. – Análise Combinatória e Probabilidade. Coleção do Professor de Matemática.

Nenhum comentário:
Postar um comentário